ML4835復(fù)合PFC/CFL小型熒光燈基于Matlab的電

摘要：介紹了一種使用Matlab仿真電力電子電路的一般性方法。該方法可以得出電力電子電路的大信號非線性仿真模型，為電力電子電路的仿真研究提供了一種方便、快捷的手段。

關(guān)鍵詞：仿真非線性模型Matlab

1前言

Matlab軟件應(yīng)用廣泛，特別是它的可開發(fā)的Simulink工具箱給各行業(yè)的工程技術(shù)人員提供了便捷的實(shí)驗手段。對于電力電子拓?fù)?，由于它的非線性可以使用Simulink中的開關(guān)模擬，因此通過分段分析電路拓?fù)?，然后使用開關(guān)來切換各段電路就可以得出一個完整的電路的仿真模型。本文以Sheppard?Taylor拓?fù)鋄1]為例敘述其實(shí)現(xiàn)方法及應(yīng)注意的問題，最后給出結(jié)論。

2建立非線性仿真模型的一般性規(guī)則

在電力電子電路中通常含有高頻開關(guān)（如MOSFET等），給電路引入了非線性。對此類非線性，在分析電路時比較常用的方法是狀態(tài)空間平均法[2]，即首先對電路的一個開關(guān)周期進(jìn)行分段，如果電路中的電感電流工作在連續(xù)模式下，則分成Ton和Toff兩段；否則分成Ton、Toff1和Toff2三段。然后分段對電路中的儲能元件（如L、C）列寫狀態(tài)方程式。當(dāng)電感電流連續(xù)時有兩組狀態(tài)方程，電感電流斷續(xù)時有三組狀態(tài)方程。最后對所列狀態(tài)方程組按開關(guān)動作占空比和電流斷續(xù)時間比（電流斷續(xù)時）做加權(quán)平均，形成一個新的狀態(tài)方程組，并基于此對電路進(jìn)行分析。由于它抓住了高頻開關(guān)動作對低頻元件的加權(quán)平均等效性，可以較好地描述電路特性。狀態(tài)空間平均法的優(yōu)點(diǎn)是：可以得到代數(shù)描述，便于系統(tǒng)分析和綜合。不足之處在于它的出發(fā)點(diǎn)是線性展開，因而得到的是小信號模型，且過程較繁。本文針對它的不足，利用Matlab求解非線性方程的能力，根據(jù)非線性方程組直接構(gòu)造大信號仿真模型，并基于此對電路進(jìn)行分析。

2?1建立非線性方程組

此過程采用基本的電路方法，毋庸贅述，下面以例示之。對于圖1所示Sheppard?Taylor電路（兩開關(guān)同時動作）按電感L1電流斷續(xù)而電感L2電流連續(xù)分別可得狀態(tài)方程組：=Aix＋Biu(i=1,2,3)(1)

式中： x=[iL1,uC1,iL2,uO}T u=USA1=

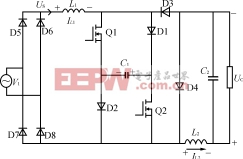
圖1Sheppard?Taylor拓?fù)?

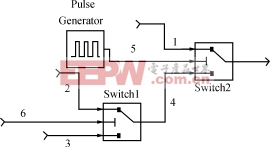
圖2關(guān)聯(lián)矩陣關(guān)系的實(shí)現(xiàn)

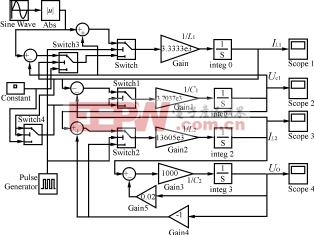
圖3Sheppard?Taylor拓?fù)浞蔷€性仿真模型的Matlab實(shí)現(xiàn)

A2=A3=B1=B2=B3=

2?2建立非線性關(guān)聯(lián)矩陣E，F(xiàn)

E=[mI?pI?qI][A1?A2?A3]T

=mA1＋pA2＋qA3(2)

F=[mI?pI?qI][B1?B2?B3]T

=mB1＋pB2＋qB3(3)

式中：[mI?pI?qI]為n×3n矩陣

[A1?A2?A3]T為3n×n矩陣

[B1?B2?B3]T為3n×n矩陣

n為Ai的階數(shù)。

2?3構(gòu)造仿真模型

由于電路工作時是在狀態(tài)方程組中分時切換，因此可以通過式（1）、（2）、（3）得到非線性仿真模型：=Ex＋Fu(4)

式中E，F(xiàn)如公式（2）、（3）。

仿真模型（4）在形式上與狀態(tài)空間平均法雖有相似之處，但存在本質(zhì)的差異。本方法在構(gòu)造出模型（4）時沒作任何忽略和線性近似（狀態(tài)空間平均法是基于小紋波近似），因此是非線性大信號模型。

3關(guān)聯(lián)矩陣的實(shí)現(xiàn)

上述仿真模型可以使用Matlab的Simulink工具箱方便實(shí)現(xiàn)。值得指出的是切換陣[mI?pI?qI]的實(shí)現(xiàn)。在本質(zhì)上m，p，q是切換時間，其中m取決于開關(guān)占空比D，而p，q的總和為開關(guān)的占空比D′(D′=1－D)。但p，q的切換時刻與狀態(tài)和電路參數(shù)有關(guān)。使用switch開關(guān)描述的關(guān)聯(lián)矩陣的實(shí)現(xiàn)方法如下：

開關(guān)切換如圖2所示。使用一個脈沖發(fā)生器來模擬開關(guān)占空比D。switch2當(dāng)5路信號為高時選通1路，否則選通4路。因此對于m，p之間的切換發(fā)生在脈沖發(fā)生器的高低電平變換時。而對于2路和3路的切換，根據(jù)電路電感中電流的斷續(xù)點(diǎn)進(jìn)行，switch1當(dāng)工作在斷續(xù)狀態(tài)的電感中有電流時選通2路，否則選通3路。其中開關(guān)switch1和switch2的閾值分別設(shè)為0和1即可。

4基于Matlab仿真實(shí)現(xiàn)和結(jié)果

以圖1拓?fù)錇槔?dāng)其工作在DCM?CCM方式時，電感L1工作在斷續(xù)模式，而電感L2工作在連續(xù)模式，兩MOSFET管工作在同步狀態(tài)（即同時開通、同時關(guān)斷）。當(dāng)MOSFETS開通時，電源給電感L1儲能，電容C1給負(fù)載提供能量；當(dāng)MOSFETS關(guān)斷時，電感L1的能量經(jīng)D1，D2流入電容C1給其充電。在其中某一時刻電感L1的電流下降為零，而電感L2一直工作在連續(xù)方式。仿真模型具體的Simulink實(shí)現(xiàn)如圖3所示。

用圖3進(jìn)行仿真可以直觀地得出電感L1、L2的電流波形和電容C1、C2上的電壓波形，且電容C2的

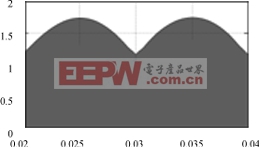
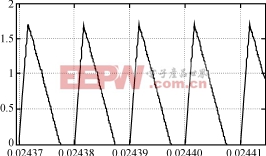
圖4仿真結(jié)果

(a)電感電流iL1的周期波形(b)電感電流iL1的局部放大波形

電壓即是輸出電壓。從圖4(a)、圖4(b)電感L1的電流可以看出電感L1是工作在斷續(xù)狀態(tài)且實(shí)現(xiàn)了PFC。圖4(a)中在nπ(n=1,2,3...)時刻電流未到零主要是其工作在斷續(xù)開環(huán)的緣故。

電路參數(shù)如下：L1=300μH，L2=735μH，C1=270μF，C2=1000μF。輸入US=110|sin(100π)|，工作頻率是fs=100kHz，D=0.169。

從圖4(c)、圖4(d)可以看出非線性模型的結(jié)果與平均模型的穩(wěn)態(tài)結(jié)果（圖略）吻合的很好。

5結(jié)語

使用狀態(tài)空間平均法可以獲得非線性開關(guān)系統(tǒng)的小信號線性化模型，但是推導(dǎo)較復(fù)雜。本文通過建立電路的狀態(tài)方程組，獲得非線性仿真模型，然后使用Matlab進(jìn)行分析。此方法具有以下的一些優(yōu)點(diǎn)：該模型是基于電路的原始非線性方程，是一個完全的非線性系統(tǒng)，具有大信號模型的特點(diǎn)。使用該方法的另一個顯著的優(yōu)點(diǎn)是構(gòu)造簡捷。只需要通過對電路列出兩組（電流斷續(xù)三組）方程，然后使用Simulink中的switch開關(guān)就可以方便地構(gòu)造出來，并可以很直觀地獲得電路的仿真結(jié)果，對電路的CAD具有一定指導(dǎo)意義。不足之處是本方法屬于結(jié)構(gòu)性描述而非代數(shù)描述，不適于系統(tǒng)綜合。